Negative Meniscus Convex-Concave Lens
For pricing, technical or any other questions please contact the supplier
- No registration required
- No markups, no fees
- Direct contact with supplier
Contact Supplier
How to order?
-
Ships from:
China
-
Sold by:
-
On FindLight:
since 2015
Description
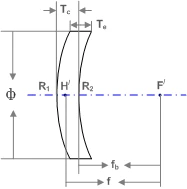
The Negative Meniscus (Convex-Concave) Lens is an essential component in advanced optical systems, meticulously designed to minimize spherical aberration. This lens features a unique shape with a smaller center thickness, allowing it to effectively increase the focal length and decrease the numerical aperture (NA) when used in combination with other lenses. Its design is particularly advantageous in applications where light needs to be diverged, ensuring that the convex surface faces the beam to achieve optimal performance.
Each Negative Meniscus Lens is crafted with precision, offering focal lengths ranging from -100.0 to -1000.0 mm, with a tolerance of ±1%. The diameter of these lenses varies from 3.0 mm to 200.0 mm, providing a wide selection to suit various optical setups. The quality of the lens is evident in its surface specifications, with scratch and dig ratings of 80/50 to 20/10 and spherical surface power and irregularity measured in fringes. These specifications ensure that the lens delivers superior optical clarity and performance.
To further enhance the functionality and durability of the Negative Meniscus Lens, it can be coated with magnesium fluoride (MgF2) to protect its surface or treated with anti-reflective (AR) coatings to increase light transmission. The precise calculation of the focal length is achieved using the formula: f = (R1 * R2) / ((n-1) * (R2-R1)), where n represents the index of refraction, and R1 and R2 denote the radius of curvature for each lens surface. This meticulous attention to detail ensures that each lens delivers impeccable performance in demanding optical applications.
Negative Meniscus Convex-Concave Lens
Specifications |
|
|---|---|
| Material: | BK7, FS, UVFS, CaF2, ZnSe, Ge, H-K9L |
| Diameter: | 3 mm |
| Available Focal Lengths: | -100mm to -1000mm |
| Available Diameters: | 3mm to 200mm |
| Surface Roughness (Scratch & Dig): | 80/50 to 20/10 |
Features
- Focal Length Range: Available from -100.0 to -1000.0 mm
- Focal Length Tolerance: ±1%
- Diameter Range: 3.0 mm to 200.0 mm
- Scratch & Dig: 80/50 to 20/10
- Spherical Surface Power: 5 Fringes to 1 Fringe
- Spherical Surface Irregularity: λ/2 to λ/8
- Center Error: 5 arc minutes to 30 arc seconds
- Design Purpose: Minimizes spherical aberration in optical systems
- Combination Use: Increases focal length and decreases numerical aperture (NA) when combined with another lens
- Divergence Application: Convex surface should face the beam to minimize spherical aberration when used to diverge light
- Focal Length Calculation: f = (R1 * R2) / ((n - 1) * (R2 - R1)), where n is the index of refraction, and R1, R2 are the radii of curvature for each surface of the lens
- Coating Options: Can be coated with MgF2 for surface protection or AR coated to increase transmission
Applications
- Beam Expansion Systems: Used to increase beam diameter in optical setups
- Laser Divergence Applications: Ensures controlled divergence with minimal aberration
- Optical Imaging Systems: Extends focal length while preserving image quality
- Research & Development: Suitable for experimental setups requiring precise divergence control
- Optical Instrumentation: Integrated into instruments requiring negative focal lengths and high accuracy
Frequently Asked Questions
A negative meniscus lens is designed to minimize spherical aberration in optical systems and can increase the focal length and decrease the numerical aperture of the system when used in combination with another lens.
The diameter range for the negative meniscus lens is 3.0mm to 200.0mm.
The tolerance for the focal lengths of the negative meniscus lens is ±1%.
Yes, the negative meniscus lens can be coated with MgF2 to protect the surface or AR coated to increase the transmission.
The focal length of the negative meniscus lens can be calculated using the equation f= (R1*R2)/((n-1)*(R2-R1)), where n is the index of refraction and R1,R2 is the radius of curvature for each surface of the lens.