cosmological parameters estimation from observing supernovae

In order to understand the contribution of matter, radiation, and dark energy in the universe, cosmologists have developed a set of cosmological parameters: matter (Ωm), radiation (ΩR), dark energy (ΩΛ). For example, in a radiation dominant universe, the value of the ‘radiation’ cosmological parameter is much greater relative to the other two parameters. According to researchers, it is theorized that we live in a dark energy dominated universe. In order to confirm this theory, the supernova cosmological project (Union 2.1) explored the contribution of each parameter by estimating their values. Another variable that can be used to determine whether we live in a matter, radiation, or dark energy dominated universe is known as the equation of state, ω. Formally speaking, the equation of state is defined as the ratio of the pressure to the energy density in a fluid. Shortly after the big bang, the universe was too hot for neutral atoms to form. Hence, the universe was dominated by radiation and ω had a value close to 1/3. At around 47,000 years after the big bang, the matter-energy density surpassed the radiation density. This resulted in the formation of all the matter we see today. Hence, the universe at this stage was classified as matter dominated and ω had a value of 0. Today, however, researchers have concluded that an unknown energy source, dark energy, is responsible for accelerating the expansion of the universe. It is theorized that 9.6 billion years after the big bang, the universe was dominated by dark energy and the equation of state since then has a value close to -1.

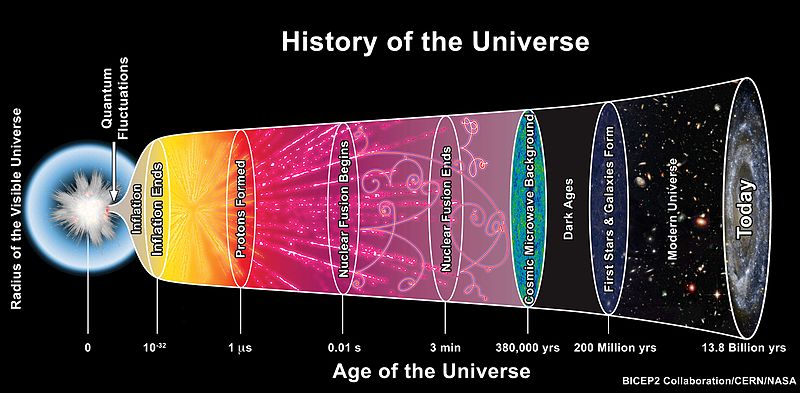
This illustration gives a brief overview of the timeline of our universe. As noted, shortly after the big bang, nucleosynthesis was the main source of complex atom production. However, due to inflation, nuclear reactions stopped. After the inflation, the dynamics of the universe were dictated primarily by radiation. Around 47,000 years after the big bang, the density of matter surpassed the density of radiation resulting in the rise of a matter dominated universe. Cosmic Microwave background (CMB) refers to the time in the universe when baryons, mainly protons, converted from being ionized to neutral. After this epoch, stars and galaxies started to emerge and dark energy fueled the expansion of the universe.

Standard Candles

Standard Candles can be described as celestial objects in space whose luminosities and relative magnitudes can be used to compute their distances. For example, Cepheid variable stars are considered Standard Candles because their pulsation allows us to measure their period. Since the pulsation period of a Cepheid variable star can be used to measure its luminosity, measuring its apparent magnitude allows us to calculate its distance. On a similar note, the explosions of stars can also be represented as standard candles. In particular, the intrinsic luminosity of a Type 1a supernova can easily be calculated and since all SNe 1a are of similar intrinsic luminosities, simply obtaining their apparent magnitude allows us to calculate the distance. In addition to measuring their apparent magnitudes, measuring the redshifts helps us estimate the cosmological parameters. In the supernova cosmology project, scientists used the observed values of the distance modulus for various SNe 1a (Union 2.1) and estimated the cosmological parameters (Ωm, ΩΛ) and the equation of state (ω) by utilizing numerical fitting techniques.

One example of a standard candle is Type 1a supernova. This particular image represents a nebula, or a Type 1a supernova remnant that was observed using the Chandra X-ray Observatory. Courtesy of google images.

Cosmological Parameters

In the project, researchers explored how the observed apparent magnitudes of Type 1a supernovae be used to estimate several cosmological parameters. In particular, they tried to fit the observed distance modulus of supernovae to its theoretical model that depended on luminosity distance. Luminosity distance is the calculated distance of an object obtained from its apparent and intrinsic magnitudes. For nearby celestial objects, luminosity distance gives a good approximation of their actual distance.

Since luminosity distance directly depends on cosmological parameters, fitting the data allowed researchers to estimate these parameters. This project was divided into three parts. The first part dealt with estimating two cosmological parameters (Ωm, ΩΛ) by holding a fixed value for the equation of state ω. This case assumed that the universe is not flat; therefore, the sum of Ωm and ΩΛ did not necessarily equal to one. In addition to obtaining the most likely values for cosmological parameters, the other goal of this case was to understand the curvature of the universe. Curvature of the universe can be split into three different possibilities: flat (no curvature), open (negative curvature), and closed (positive curvature). If the sum of all the cosmological parameters equals to one, then the universe is considered flat. If the sum is greater than one, then there is positive curvature. If the sum is less than one, then there is negative curvature. The second case dealt with estimating the cosmological parameters and the equation of state by assuming that the universe is flat. Recall that in a flat universe, ΩΛ = 1 – Ωm, solving for just the matter cosmological parameter allowed them to obtain the value of dark energy cosmological parameter. The third case dealt with estimating a single parameter by holding other parameters fixed. For example, in one particular case, they estimated the likelihood of the equation of state, ω, by assuming a flat geometry (Ωm + ΩΛ = 1) and approximating Ωm and ΩΛ to be 0.3 and 0.7 respectively. All of these cases did prove that the acceptable values of Ωm, ΩΛ, and ω are 0.3, 0.7 and -1 respectively. This analysis confirms that we do, in fact, live in a dark energy dominated universe.

References