Optical Neural Networks: The Future of Deep Learning?

Optical Neural Networks can revolutionize data science. The current state of data science places a heavy emphasis on large quantities of data, which are widely available due to increased computational power and progressively sophisticated cloud infrastructure that enable proliferated data generation and sharing. However, traditional CPUs are starting to reach the limit of what they can achieve in the realm of data processing and deep learning. For those new to deep learning, it is a type of machine learning that utilizes artificial neural networks in which multiple layers of processing are used to extract increasingly higher level features from data.

Artificial neural networks are systems that attempt to computationally imitate the biological neural network present in human brain. Current artificial neural networks are coming with limitations with large processing times and energy consumption. As a result, there is a lot of research into alternative methods. An optical neural network (ONN) attempts to do this with optical structures to improve the efficiency and speed. In this blog post, we will introduce how ONNs work, we will look at some examples as well as at their benefits and drawbacks.

1. What is a Neural Network?
2. How does an Optical Neural Network work? 
3. Examples of Optical Neural Networks
4. Benefits and Drawbacks of Optical Neural Networks

What is a Neural Network? 

Simply put, an artificial neural network (NN) attempts to imitate the brain computationally in performing logical functions. Within the brain, neurons send electrical and chemical signals to each other via synapses at the end of a long axon. The signal is then received by the dendrites of another neuron, which branch out at the end of a neuron. These neurons allow the brain to store and pass information, as well as learn what the information means. In the following three section let’s look into three types of NNs, which all work under the same principle.

Artificial Neural network (ANN)

The first, and most basic is a feedforward Artificial Neural Network (ANN). In this system the input, X, is matrix multiplied with a predetermined weight matrix, W. This matrix contains information about the relevance of each element of the input for finding the correct solution. For instance, when identifying an image of a cat, the ears and tail may hold more relevant information than the paws or stomach.

A nonlinear activation function, f, is applied to the resulting vector, Z, usually a ReLU or sigmoid function. This nonlinearity is important for the ANN, as it typically normalizes the outputs to 0 or 1, giving more digestible information. In the example of identifying a cat, the activation function may convert all the pixels associated with the cat to 1 and all the background pixels to 0. The output of this single layer then becomes the input for the next layer. Each hidden layer is analogous to a biological neuron, where input signals are interpreted and then passed to the next layer or neuron.  The image below shows an illustration of a neural network. 

A key feature of Neural Networks is the training, which is done either by forward propagation or back propagation. Back propagation consists of sending the output back through the layers to determine how well the NN performed. With each back propagation, the weights and biases are altered so the next iteration will perform better. For electronic neural networks, this is programmed with a CPU.

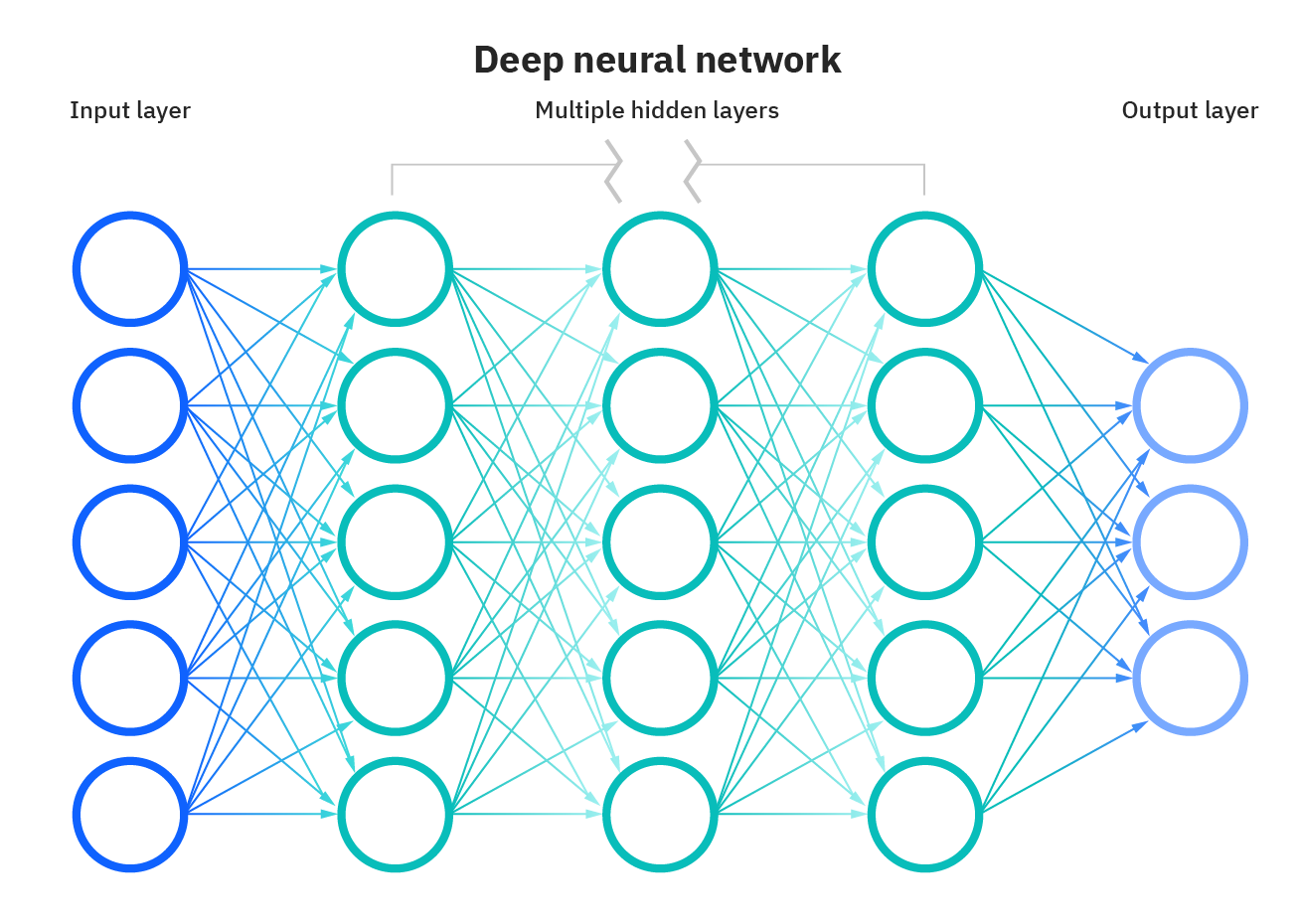
Illustration of a the inputs, hidden layers, and outputs of a neural network. Courtesy of IBM.

Recurrent Neural Network

Another type of NN is a recurrent neural network (RNN). This works in much the same way, except the output of past examples are accounted for when calculating future examples. This can be useful in areas where time sequence is important, like in music, where sequences of notes are relevant. Also, in cases that involve communication, a RNN is useful, because language has many sequential characteristics (e.g. adjectives describe nouns and, specifically in English, often come before the noun being described). Using this knowledge and implementing a RNN for speech recognition will likely give a better result than a basic ANN.

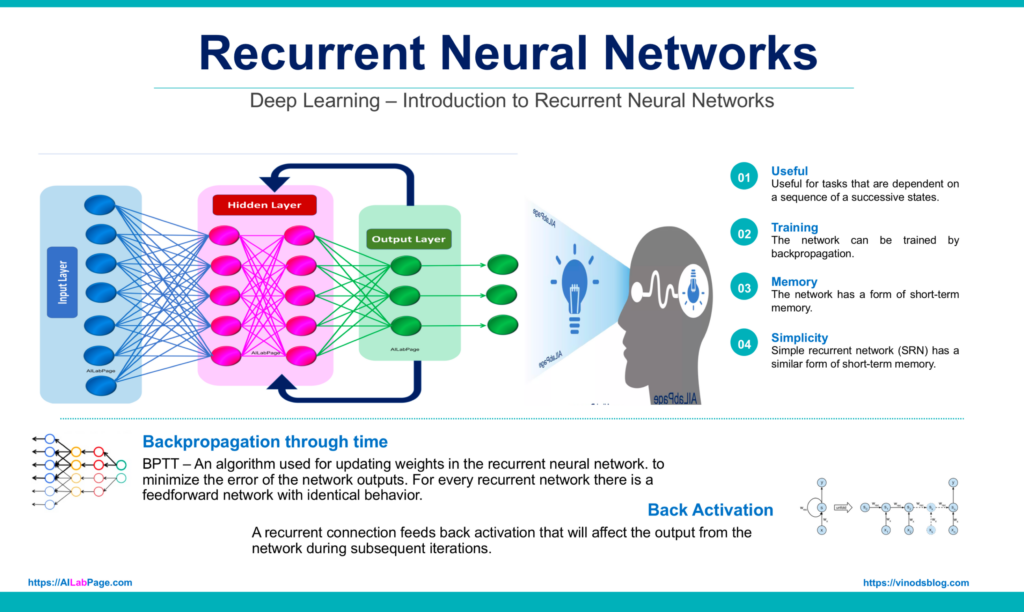
Schematic representation of Recurring Neural Networks (RNN)

Convolutional Neural Network

Another major type of NN is a convolutional neural network (CNN), which is often used for computer vision and image analysis. Like the RNN, this architecture uses the intra-dependencies within the data to improve the model output. However, unlike an RNN, the CNN uses convolution to determine how the values in a single example are dependent on each other, rather than how an example is dependent on other examples. For instance, an image can be thought of as a matrix of pixels. In some cases, a pixel is related to the pixels surrounding it, which makes the information resulting from a convolution relevant. This convolution step also helps reduce the computational requirements of the system as it stores the information in a smaller matrix.

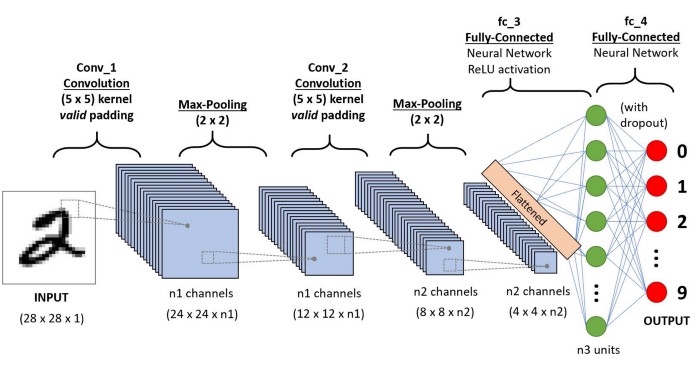
A CNN sequence to classify handwritten digits. Courtesy of TowardsDataScience

Other Neural Networks

There are several other types of neural network, many of which fall under the categories listed above. A variation of the RNN is a long short-term memory NN, which can maintain a memory of the input and output information. This memory cell had three gates which control which information can enter the memory cell, which information can be passed to the next layer, and which information is forgotten. Another type of NN, the Modular neural network, consists of several neural networks that perform various tasks independently and simultaneously. This is useful for tasks that require separate computations on the same input data, such as stock market predictions.

How does an Optical Neural Network work?

Much like electronic neural networks, Optical Neural Networks (ONN) perform mathematical operations on input signals and pass them through several layers. Some of the key features of a NN, performing weighted matrix multiplication, and applying a linear bias term and nonlinear activation function, can be performed by utilizing the properties of optical structures.

As we know from Fourier Optics, a lens can perform a Fourier transform on a signal. And, by the convolution theorem, we know that the Fourier transform of a convolution is equivalent to the multiplication of Fourier transforms:

F{f ∗ g} = F{f} ·F{g} 

Here f and g are functions and F{f} is the Fourier transform of f. Thus, by passing a signal through a lens and then performing linear operations, one can essentially perform a convolution on the signal. 

Nonlinearities are easy to introduce using saturable absorbers or amplifiers, dyes, and semiconductors. These usually require no additional energy to function.

Examples of Optical Neural Networks

Let’s look into three examples of ONN architecture.  Each of these architectures has a different approach, from using lenses and light beams to waveguides and interferometers.

Multi-layer optical Fourier neural network

One way to transmit signals optically utilizes lenses and transmission masks to focus the light and manipulate the intensity of the beam. This process is used in the design by Q. Wu. Here, they design an ONN to interpret handwritten digits. Their signal is first expanded with two lenses, and then passed through programable spatial light modulators (SLMs). The weight matrix is loaded onto the SLMs through a CPU. Two of the lenses, L5 and L6, form a convolutional system, followed by an inverse Fourier transform. The light is then collected on a CCD, which is divided into 10 regions each representing one of the handwritten numbers the ONN could receive.  

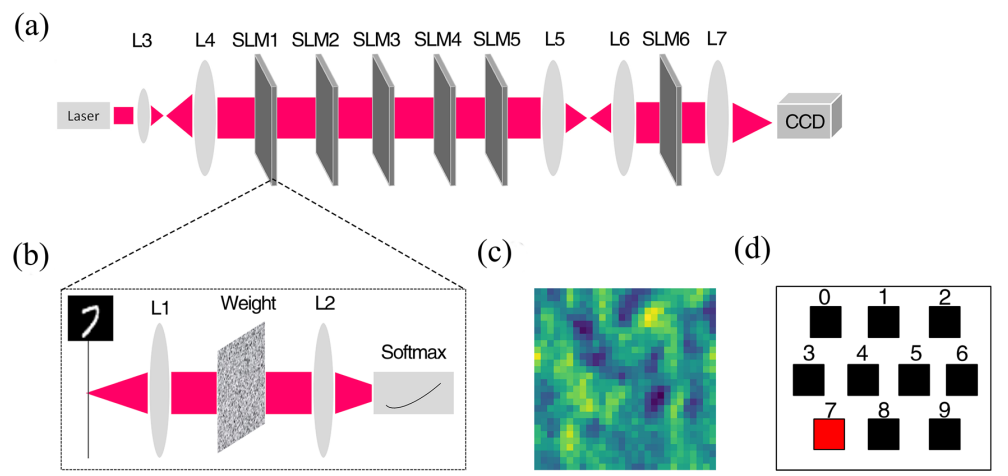
(a) & (b) Schematic of the Fourier ONN design. (c) Example of a weight mask. (d) Regions on the CCD for differentiating handwritten digits. Courtesy of AIP Advances.

Coherent Nanophotonic Circuit

In this example, the authors propose a two-layer ONN architecture to identify spoken vowels. The voice signal is multiplied by a Hamming window (a mathematical function that is close to zero outside of some chosen interval) and then converted to frequency with a Fourier transform. They do this by using Optical Interface Units (OIU), the on-chip system that interacts with light in this network, to implement weighting on the input signal. Within the OIU, shown below, tiny Mach-Zehnder Interferometers (MZI), composed of directional couplers and programable phase shifters, perform the matrix multiplication and attenuation. They then send the signal to a CPU to simulate a saturable absorber, which acts as the activation function. 

An optical micrograph of a single Optical Interference Unit featuring 56 tiny MZIs. Courtesy of Nature Photonics.

Complex-Valued Optical Neural Network

The ONN design described in this paper, uses a similar method, and was likely building off the previous example. While they also use MZIs to perform matrix multiplication, their architecture uses optical interference to perform complex valued arithmetic on a single optical neural chip, shown below. This allows the system to perform better than systems that only look at real values. In the schematic below, the red area indicates signal preparation. Reference light is passed through the green section, to be used in signal detection, marked by black. And the blue section in the middle is the area where matrix multiplication is realized. 

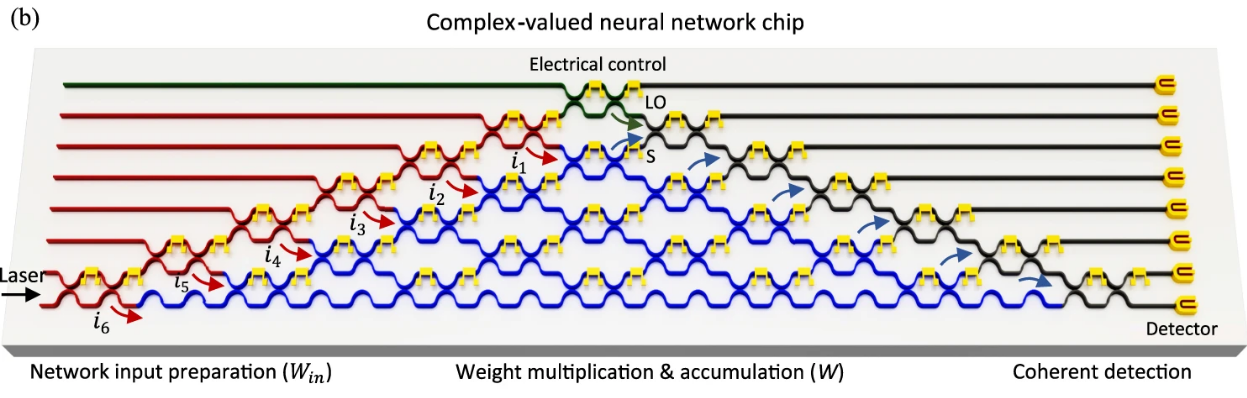
Micrograph describing the elements of the the Complex value Optical Neural Network. Courtesy of Nature Communications.

The illustration below describes the workflow of the proposed architecture. The incident signal is first split into the signal light and reference light. The signal light then passes through the modulator, which is designated by the task, and the ONN before being compared to the reference light in the Coherent Detection section. In this system, the interference of the signal and reference light performs the matrix multiplication. An activation function is applied during the Classical Processing section and the weights are readjusted depending on the error of the network.

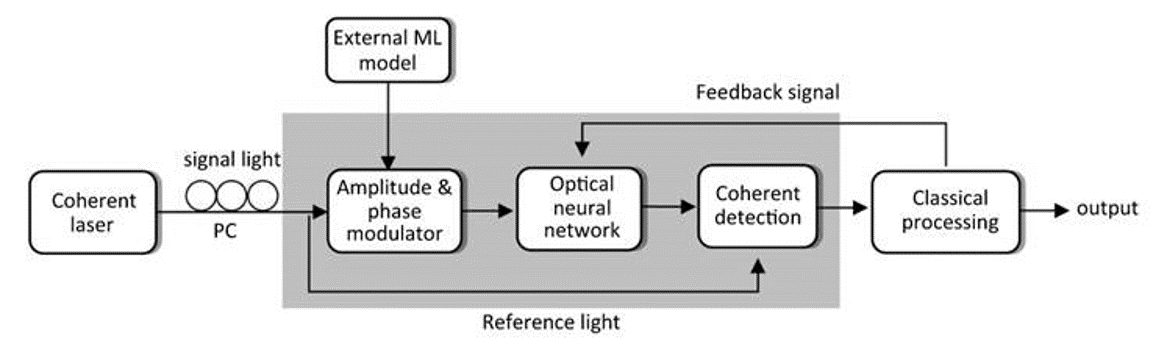
An illustration of the experimental workflow for the complex valued Optical Neural Network. Courtesy of Nature Communications.

Benefits and Drawbacks of Optical Neural Networks

There are many benefits to using ONNs over the electronic counterparts. One of these benefits is the potential computational speed that can be achieved when working with light, since optical signals travel at the speed of light in vacuum. Further, as electronic systems are getting smaller, Moore’s Law, which states that “the number of transistors in a dense integrated circuit (IC) doubles about every two years”, is slowing down. Some attribute this slow to the increase in complexity of systems being designed. ONNs pose a potential solution to this threat.

Several of the proposed ONN architectures require a CPU to function. This dependence is one of the main downsides of ONN designs, as it slows the process down. More research into ways to reduce CPU dependence and eventually eliminate the dependence entirely is necessary. While some elements, like lenses require no energy input, others like the SLMs and MZIs do require energy. This becomes a problem when trying to scale up the ONN designs.

There is still a lot of research needed to understand just how much ONNs can contribute to deep learning. Some believe that this research needs to happen immediately or while electronic deep learning models are struggling. Otherwise, ONNs will have missed their opportunity since their electronic counterparts are being actively improved by many large companies.

This article was brought to you by Zolix Instruments - supplier of scientific instruments and analytical solutions for material science and other applications